Int J App Pharm, Vol 17, Issue 4, 2025, 471-482Original Article

AN INVESTIGATION ON CERVICAL CANCER DRUGS THROUGH QSPR MODEL EMPLOYING DEGREE-RELATED TOPOLOGICAL INDICES

PRIYADARSHINI S.^*, S. KOPPERUNDEVI

Department of Mathematics, Dr. M. G. R. Educational and Research Institute, Maduravoyal, Chennai-600095, India
^*Corresponding author: Priyadarshini S.; ^*Email: priyasundar2404@gmail.com

Received: 18 Mar 2025, Revised and Accepted: 20 May 2025

---

ABSTRACT

Objective: To explore the relationship between topological indices and physical properties of the drugs administered for the treatment of cervical cancer using Quantitative Structure–Property Relationship (QSPR) modelling. The present study hopes to determine whether mathematical descriptors of drug molecules can predict physical properties without needing laboratory testing.

Methods: Topological index, used as a molecular descriptor, was employed to describe the molecular structure of gemcitabine, vinblastine, irinotecan, and topotecan, among other cervical cancer drugs. QSPR was just about to find a mathematical relationship between their molecular descriptors and the physical properties like boiling point, molar refractivity, and flash point. Topological Indices: Nine topological indices were used for the molecular structure analysis of each drug. The correlation coefficients and *p-values were calculated to test the significance of these relationships statistically.

Results: The statistical analysis defined the relationships between topological indices and physical properties to be statistically significant when the correlation coefficient referred to was more than 0.7, with a *p-value of less than 0.05. The conditions for the results of this study were satisfied, thus ensuring strong and meaningful correlations.

Conclusion: The study shows that topological indices can be effectively incorporated into QSPR modelling to predict the physical properties of drugs against cervical cancer. If provided with mathematical tools, chemists and medical practitioners may find it useful for drug design and development, thereby decreasing the dependence on long-duration, tedious, and expensive laboratory experiments.

Keywords: Cervical cancer drugs, Topological indices (TIs) based on degree, QSPR analysis, Linear regression model

---

© 2025 The Authors. Published by Innovare Academic Sciences Pvt Ltd. This is an open access article under the CC BY license (https://creativecommons.org/licenses/by/4.0/)
DOI: https://dx.doi.org/10.22159/ijap.2025v17i4.54256 Journal homepage: https://innovareacademics.in/journals/index.php/ijap

INTRODUCTION

Cervical cancer is a common malignancy in women, causing abnormal behaviour in cells at the cervix due to small DNA changes. In 2022, cervical cancer could have advanced more rapidly in women with untreated HIV and impaired immunity, with 660,000 new cases and 350,000 deaths due to the disease. Human Papillomavirus (HPV) is implicated in about 95% of cervical cancer cases. Other risk factors include smoking, obesity, multiple pregnancies, young age, hormonal contraceptives, and a weak immune system. Early detection and treatment can help recover from cervical cancer.

There are four basic stages of cervical cancer: Stage I, where the cervix is the only affected area; Stage II, where the uterine tissues are affected; Stage III, where kidney issues or the lower part of the vagina are affected; and Stage IV, where cancer has spread irrespective of the pelvis [1]. Cervical cancer can be treated through various forms of therapy, which include radiotherapy, chemotherapy, and surgery. There are also new classes of therapies, targeted treatments, and immunotherapy [2]. HPV, which can be prevented through vaccination, like Cervarix and Gardasil. Effective treatment starts with early diagnosis through screening tests. It is through awareness and risk assessment that prevention and timely interventions can be done. Advances in pharmaceutical sciences will continue to improve outcomes in treatment by creating more potent medications and therapies for cervical cancer.

Significant impact is made in improving patient care and survival rates by these developments [3]. There are also studies done on various anticancer medicinal plants, their active compounds, and mechanisms of action, including apoptosis induction and immune modulation, and they suggest that the efficacy of herbal therapy in cervical cancer is enhanced when it is integrated with conventional treatments to offset side effects and improve patient outcomes [4].

It is a representation in which structural descriptors expressed as numerical indices are translated from the molecular structure. Predicting physical properties is aided by these numerical values. There are degree, distance, and spectral-related topological indices. Broadly, these topological indices are applied in Quantitative Structure-Property Relationship (QSPR) and Quantitative Structure-Activity Relationship (QSAR) modelling, providing information that scientists need to know about the characteristics of molecular structures that are useful for manufacturing any drugs. Physical, biological, and chemical attributes can be learned from this approach.

Degree-based topological indices have been selected over other TIs for this investigation due to their intrinsic simplicity, intuitive interpretability, and ease of calculation, which is extremely useful in QSPR modelling. The computational efficiency of these indices has allowed for rapid screening of molecular structures without the necessity for a comprehensive 3D conformational analysis. Moreover, in the recent past, these TIs have been reported to accurately predict physical and chemical properties, especially concerning drug development modelling. This study extends the earlier QSPR efforts in oncology by focusing only on molecules that treat cervical cancer, using a unique combination of degree-based metrics that have not been thoroughly explored in earlier studies. The selected anticancer drugs and the modelling framework are customized for this application and offer a more focused and possibly effective approach than more general or less specific oncology QSPR models.

This article inspects the physical characteristics of cervical cancer drugs using degree-based TIs. A detailed evaluation is performed using the QSPR model. Utilizing the linear regression model, these TIs and drug features have been estimated; refer to fig. 1. This method shows good correlation with the physical qualities of cervical cancer drugs and TIs using a regression model.

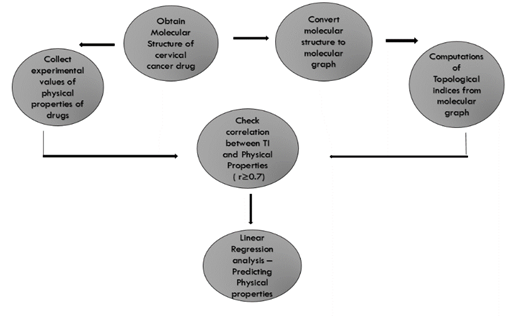
Fig. 1: Technique for results computation

Articles about various drugs to treat different kinds of disorders are published in many places using TI based on degree and linear regression analysis. The articles inspired me to work on cervical cancer treatments using this approach. Recently, focusing on QSPR modelling employing degree-based indices to predict physicochemical attributes of twenty eye infection drugs, operated on nine indices, where the first and second revised Randic indices had a good correlation with the essential drug properties [5]. QSPR analysis studied the properties of 21 breast cancer drugs and worked on eleven indices, which established strong correlations between selected indices and six drug properties [6].

Also performed on different drugs that are used in anti-cancer and anti-malaria disorders by the QSPR model with the same strategy, seventeen drugs on thirteen TIs and nine drugs on seven TIs, respectively [7], [8]. With the application of linear regression and degree-related TIs, in the prediction of the physicochemical characteristics of the ten drugs applied in the rheumatoid arthritis treatment, nine TIs provided a significant range and were highly correlated with polarity, refractive index, molar volume, and complexity [9]. The highly correlated also predicted all the physicochemical properties with the help of nine indices of the eleven drugs used in vitiligo disease [10]. The article works towards analyzing thirteen Human Immunodeficiency Virus (HIV) treatment drugs. By utilizing nine degree-based TIs, the research establishes a correlation between the physicochemical attributes of these drugs, such as melting and boiling points, and their structural characteristics [11]. Effective usage of a linear regression model to relate the treatment indicators to drug attributes for sixteen medications used in treating hepatitis [12].

MATERIALS AND METHODS

As seen in fig. 2, chemical graph theory uses a molecular graph to represent the molecular structure of a drug developed for treating cervical cancer. In this model, the vertices represent atoms, and the edges denote the bonds between them. A vertex's degree in the molecular graph is associated with the valence in the molecular structure of the compound. The molecular graph thus consists of a vertex set V(G) and edge set E(G) given by G(V, E), and it is simple and connected, with no loops. The degree of a vertex in graph G, denoted by d_m, is determined by all the edges connecting it [13], [14]. The list below contains the degree-related TIs that were used in this paper:

Definition 2.1, 2.2: The first and second Zagreb indices, initiated by Gutman et al., are used to determine the molecules’ total pi-electron energy [15].

M₁(G)= ……. (1)

M₂(G)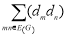₌ ………. (2)

Definition 2.3: The Randic index aids in estimating the saturated hydrocarbons' carbon atoms' branching extent. It was introduced by Randic [16].

R(G) = ………. (3)

Definition 2.4: An additional Randic index variant is the harmonic index proposed by Fajtlowicz [17].

H(G) = 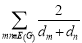………. (4)

Definition 2.5: An Atom Bond Connectivity (ABC) index is used to research the formation heat of heptanes and octanes framed by Estrada et al. [18].

ABCG) = 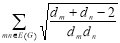….. (5)

Definition 2.6: Gutman has introduced the sombor index to provide a geometrical approach to degree-based topological indices [19].

SO(G) = 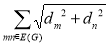………. (6)

Definitions 2.7, 2.8, 2.9: V. R. Kulli recently proposed the Nirmala index, which was inspired by the Sombor index [20]. Further, V. R. Kulli et al. introduced the first inverse nirmala index and the second inverse nirmala index, and also performed studies on certain antiviral drugs [21, 22].

N(G) =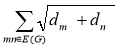 …………. (7)

N₁(G) =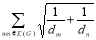 ………. (8)

N₂(G) =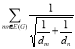………. (9)

This article involves statistical analysis and topological indices computed and required in research on drugs. The techniques include vertex degree labelling and vertex and edge partitioning to derive topological indices. Calculations of such findings are done using a scientific calculator. ChemSpider was used to extract experimental data (table 2) and the structure of drugs (fig. 2) in treating cervical cancer, and both the experimental and predicted data were compared using a linear regression model.

The selection of 14 drugs in this study rested upon two main bases: clinical relevance and availability of data. Only those drugs having an established therapeutic purpose in treating cervical cancer and their structural and physicochemical information available in reliable databases were taken into account. This assures that compounds for which credible experimental records exist for characteristics mentioned below are considered on equal grounds for assessing the topological indices presented.

(a)	(b)	(c)	(d)
(e)	(f)	(g)	(h)
(i)	(j)	(k)	(l)
(m)	(n)

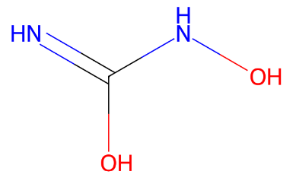
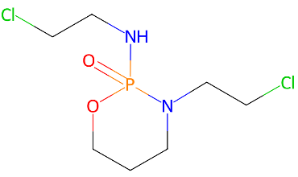
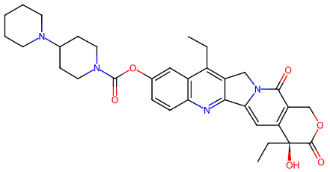
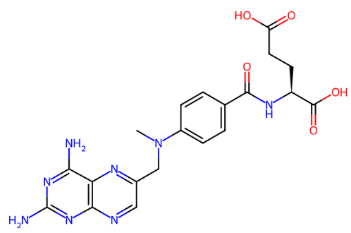
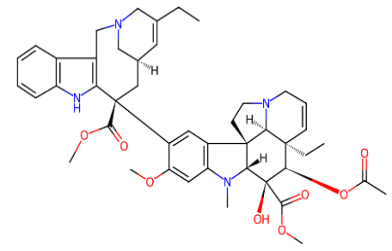
Fig. 2: (a) Ciclophosphamide (b) Doxorubicin (c) Etoposide (d) Fluorouracil (e) Gemcitabine (f) Hydroxyurea (g) Ifosfamide (h) Irinotecan (i) Methotrexate (j) Neratinib (k) Paclitaxel (l) Topotecan (m) Vinblastine (n) Vinorelbine

The molecular formulas for various compounds are as follows: Ciclophosphamide (C₇H₅ClNOP),, Doxorubicin (C₂₇H₂₉NO₁₁), Etoposide (C₂₉H₃₂O₁₃), Fluorouracil (C₄H₃FN₂O₂), Gemcitabine (C₉HFNO), Hydroxyurea (CH₄N₂O₂), Ifosfamide (C₇H₁₅Cl₂N₂O₂P), Irinotecan (C₃₃H₃₈N₄O₆), Methotrexate (C₂₀H₂₂N₈O₅), Neratinib (C₃₀H₂₉ClN₆O₃), Paclitaxel (C₄₇H₅₁NO₁₄), Topotecan (C₂₃H₂₃N₃O₅), Vinblastine (C₄₆H₅₈N₄O₉), and Vinorelbine (C₄₅H₅₄N₄O₈).

These chemotherapeutic agents work by inhibiting DNA synthesis, preventing cancer cell replication, and inducing apoptosis. Combination therapy is beneficial in enhancing efficacy; targeting advanced or recurrent cervical cancer can improve patient outcomes.

RESULTS AND DISCUSSION

TIsbased on the degree of the drugs used for cervical cancer will be calculated. These calculatedindices used in QSPR analysis will be studied in this research, and these indices reveal that a strong correlation is present with the physical characteristics of the drugs used in cervical cancer treatment.

The drugs used in this study are ciclophosphamide, doxorubicin, etoposide, fluorouracil, gemcitabine, hydroxyurea, ifosfamide, irinotecan, methotraxate, neratinib, paclitaxel, topotecan, vinblastine, vinorelbine. Here, we considered these molecular structures as graphs where the drug elements are considered as vertices and the bonds connecting them are represented as edges.

Theorem 1

Evaluate a molecular graph G for topotecan; then M₁(G) = 180, M₂(G) = 226, R(G) = 14.74,H(G) = 14.071, ABC(G) = 24.966, SO(G) = 130.961, N(G) = 79.059, N₁(G) = 32.639, N₂(G) = 38.173.

Proof

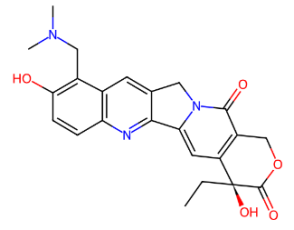
Fig. 3: Transformation of molecular depiction to molecular graph of Topotecan

In fig. 3, we can observe the transformation of molecular structure to molecular graph; there are eight different kinds of edges, altogether 35, and 31 vertices. They are as follows:

E_1,3 = { e = mn E(G)| d_m = 1, d_n= 3} = 5

E_1,4 = { e = mn E(G)| d_m = 1, d_n= 4} = 1

E_2,3 = { e = mn E(G)| d_m = 2, d_n = 3} = 1

E_1,2 = { e = mn E(G)| d_m = 1, d_n = 2} = 1

E_2,3 = { e = mn E(G)| d_m = 2, d_n = 3} = 14

E_2,2 = { e = mn E(G)| d_m = 2, d_n = 2} = 2

E_3,3 = { e = mn E(G)| d_m = 3, d_n = 3} = 9

E_3,4 = { e = mn E(G)| d_m = 3, d_n = 4} = 2

By using Definition 2.1,

M₁(G) = 5(1+3)+(1+4)+(2+4)+(1+2)+14(2+3)+2(2+2)+9(3+3)+2(3+4)

=180 ……… (10)

By using Definition 2.2

M₂(G) = 5(1 × 3)+(1 × 4)+(2 × 4)+(1 × 2)+14(2 × 3)+2(2 × 2)+9(3 × 3)+2(3 × 4)

= 226 ………. (11)

By using Definition 2.3

R(G) =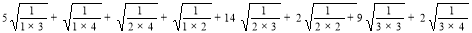

= 14.74 …….. (12)

By using Definition 2.4

H(G) =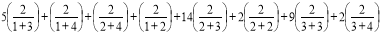

= 14.071 …….. (13)

By using Definition 2.5

ABC(G) =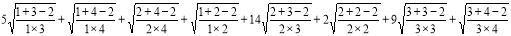

= 24.966 ………. (14)

By using Definition 2.6

SO(G) =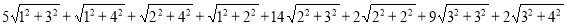

=130.961 ……….. (15)

By using Definition 2.7

N(G) =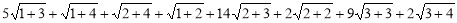

=79.059 ………. (16)

By using Definition 2.8

N₁(G) =

By using Definition 2.8

N₁(G) =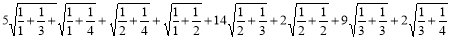

=32.639 …………. (17)

By using Definition 2.9

N₂(G) =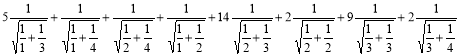

= =38.173 ………. (18)

Thus, TIs for all the other unexpended drugs can be obtained by making use of the process in Theorem 1 and applying the definitions from 1 to 9. The corresponding values for each medication are given in table 1.

Table 1: Topological indices values for the drugs for other drugs that are taken into consideration in the study and worked on by this method

Drugs	M1 (G)	M2(G)	R(G)	H(G)	ABC(G)	SO(G)	N(G)	N1(G)	N2(G)
Ciclophosphamide	64	72	6.726	6.486	9.996	46.721	29.717	13.889	14.336
Doxorubicin	220	275	18.428	17.486	30.77	160.4	96.82	40.501	46.589
Etoposide	242	302	20.282	19.63	33.88	174.559	107.399	44.553	52.434
Fluorouracil	42	46	4.198	3.933	6.651	30.98	19.393	8.931	9.205
Gemcitabine	96	119	8.374	7.354	13.835	70.764	42.496	18.292	20.164
hydroxyurea	16	14	2.27	2.067	3.047	12.167	7.968	4.447	4.052
Ifosfamide	64	72	6.726	6.486	9.996	46.721	29.717	13.889	14.336
Irinotecan	237	290	20.762	20.171	34.737	171.124	106.197	45.023	51.842
methotrexate	168	192	15.617	14.833	25.462	122.865	76.519	33.761	39.046
Neratinib	202	233	19.371	18.8	30.64	145.94	92.904	41.233	45.321
paclitaxel	346	429	29.377	27.783	48.99	253.05	152.62	62.69	75.286
topotecan	180	226	14.74	14.071	24.966	130.961	79.059	32.639	38.173
vinblastine	355	460	28.609	27.476	47.906	257.982	154.407	63.075	74.749
Vinorelbine	338	463	27.385	26.376	45.666	245.054	147.295	60.234	71.511

Table 2: The physical properties of the drugs utilised for cervical cancer

Drugs	Boiling point (°C at 760 mmHg)	Flash point (°C)	Molar volume (cm3)	Enthalpy of vaporization (kj/mol)	Molar refraction (cm3)	Polarizability (cm3)
Ciclophosphamide	336.1	157.1	195.7	57.9	58.1	23
Doxorubicin	810.3	443.8	336.6	123.5	131.5	52.1
Etoposide	798.1	263.6	378.5	121.7	140.1	55.5
Fluorouracil			84.8		25.9	10.2
Gemcitabine	482.7	245.7	142.3	86.2	52.1	20.6
Hydroxyurea	222.1	88.1	43.9	53.3	13.8	5.5
Ifosfamide	336.1	157.1	195.7	57.9	58.1	23
Irinotecan	873.4	482	416.8	133	159.2	63.1
Methotrexate			295.7		119	47.2
Neratinib	757	411.6	416.8	110.3	155.1	61.5
Paclitaxel	957.1	532.6	610.6	146	219.3	86.9
Topotecan	782.9	427.3	281.3	119.5	112.7	44.7
Vinblastine			590		220.7	87.5
Vinorelbine			569.7		214.2	84.9

In this article, table 1 presents data that reflects a normal distribution. The fact that statistical data is significant when the*p-value is less than 0.005 and the r-value is more than 0.7. So, as a direct consequence of these results, all the concerned properties are found to be significant.

Therefore, the ideal model to look at and apply in this analysis is the linear regression model. We recommend [5-12, 23, 25] for more information on TIs.

Regression models

The examination workout was done on 9 indices: such as M₁(G), M₂(G), R(G), H(G), ABC(G), SO(G), N(G), N₁(G), and N₂(G). The six physical properties are used to model these indices: boiling point (BP) °C at 760 mmHg, flash point (FP) °C, molar volume (MV)cm³, enthalpy of vaporization (EV) kj/mol, molar refractivity (MR) cm³, polarizability (POL) 10^-[24] cm³. For the drugs, regression analysis has been conducted, and the linear regression model has been evaluated using this equation.

P = A+b (TI) …. (19)

Where P is Physical property, TI is topological indices, A is a constant, and b is a regression coefficient. Nine topological indices of the defined molecular structure are regarded as independent variables, while the six physical characteristics of the drugs used to treat cervical cancer are regarded as dependent variables.

The linear regression equation's A and b are determined using the training set in tables 1 and 2 when the linear regression model is calculated using SPSS software. The models are available below for the linear regression equation for each index (19).

(I) Regression model of M1(G): Boiling point = 223.655+2.471 [M1 (G)] Flash Point = 94.432+1.358[M1 (G)] Molar volume = 39.474+1.559 [M1 (G)] Enthalpy of vaporization=47.459+0.321[M1 (G)] Molar Refraction = 8.921+0.605 [M1 (G)] Polarization = 3.514+0.24 [M1 (G)]	(V) Regression model of ABC(G): Boiling point = 209.78+17.679 [ABC (G)] Flash Point= 85.29+9.782[ABC (G)] Molar volume= 22.046+11.594[ABC (G)] Enthalpy of vaporization= 45.826+2.288[ABC (G)]Molar Refraction= 2.146+4.501[ABC (G)] Polarization= 0.828+1.785[ABC (G)]
(II) Regression model of M2(G): Boiling point = 236.936+1.962[M2 (G)] Flash Point= 102.628+1.074[M2 (G)] Molar volume= 59.334+1.167[M2 (G)] Enthalpy of vaporization= 49.009+0.256 [M2 (G)] Molar Refraction = 16.666+0.453[M2 (G)] Polarization= 6.586+0.18[M2 (G)]	(VI) Regression model of SO(G): Boiling point = 223.478+3.399[SO (G)] Flash Point= 93.812+1.873[SO (G)] Molar volume= 38.7+2.149[SO (G)] Enthalpy of vaporization=47.397+0.442 [SO (G)]Molar Refraction= 8.632+0.834[SO (G)] Polarization= 3.4+0.331[SO (G)]
(III) Regression model of R(G): Boiling point = 195.489+29.927 [RA (G)] Flash Point= 76.88+16.593[RA (G)] Molar volume=10.216+19.812 [RA (G)] Enthalpy of vaporization= 44.195+3.858[RA (G)]Molar Refraction=-2.236+7.678[RA (G)] Polarization=-0.91+3.044[RA (G)]	(VII) Regression model of N(G): Boiling point = 216.901+5.621 [N (G)] Flash Point= 90.598+3.092[N (G)] Molar volume= 32.14+3.596 [N (G)] Enthalpy of vaporization = 46.697+0.728[N (G)] Molar Refraction= 6.075+1.396[N (G)] Polarization= 2.386+0.553[N G)]
(IV) Regression model of H(G): Boiling point = 199.599+31.067[H (G)] Flash Point= 80.08+17.16[H (G)] Molar volume= 12.916+20.557[H (G)] Enthalpy of vaporization= 44.885+3.994[H (G)]Molar Refraction=-1.166+7.965[H (G)] Polarization=-0.486+3.158[H (G)]	(VIII) Regression model of N1(G) Boiling point = 195.419+13.878[N1 (G)] Flash Point= 77.947+7.66[N1 (G)] Molar volume=15.415+8.988[N1 (G)] Enthalpy of vaporization= 44.135+1.791[N1 (G)] Molar Refraction=-0.444+3.49[N1 (G)] Polarization=-0.2+1.384[N1 (G)]
(IX) Regression model of N2(G) Boiling point = 222.832+11.385[N2 (G)] Flash Point= 93.937+6.26[N2 (G)] Molar volume=32.648+7.363[N2 (G)] Enthalpy of vaporization= 47.444+1.475[N2 (G)] Molar Refraction= 6.25+2.858[N2 (G)] Polarization= 2.455+1.133[N2 (G)]

Comparison of topological indices based on the correlation statistical description of physical property coefficient

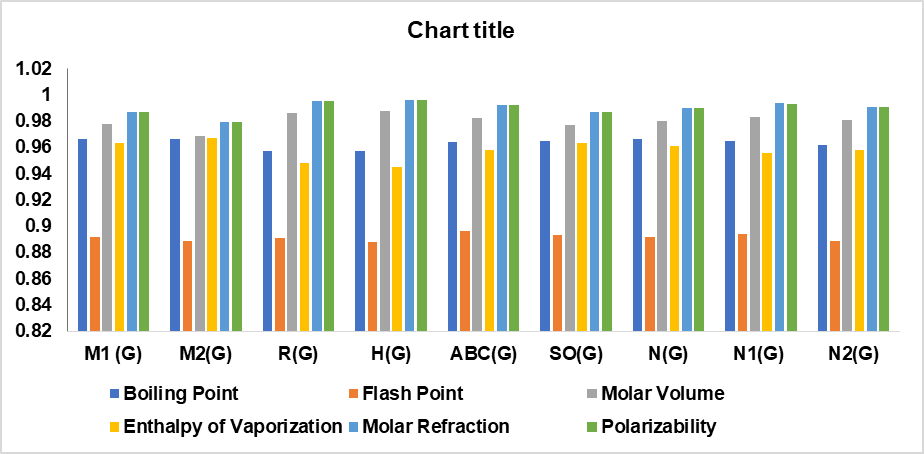
A computation of these degree-based TIs was performed for 14 cervical cancer drugs in table 1; table 2 presents their physical properties. From table 13, it can be concluded that there is an interdependence of these indices with six physical features, which considerably supports the findings here. The correlation between the topological indices and the physical characteristics of the drug, graphical representation is illustrated in fig. 4.

Table 3-11 lists various statistical parameters associated with QSPR models on TIs. Several drugs taken into consideration, constant, regression coefficient, correlation coefficient, Fisher's statistic, and possible value of significance for the QSPR model concerning all topological indices and physical properties put into consideration constitute the parameters N, A, b, r, F, and P. It will help in comparative assessments and model improvements.

Table 3: QSPR models are composed of statistical parameters for M₁(G)

Physical property	N	A	b	r	r2	F	P	Indicator
Boiling point	10	223.655	2.471	0.966	0.933	111.727	0.000	Significant
Flash point	10	94.432	1.358	0.892	0.796	31.182	0.001	Significant
Molar volume	14	39.474	1.559	0.978	0.956	257.724	0.000	Significant
Enthalpy of Vaporization	10	47.459	0.321	0.963	0.928	103.448	0.000	Significant
Molar Refraction	14	8.921	0.605	0.987	0.975	470.451	0.000	Significant
Polarization	14	3.514	0.24	0.987	0.975	467.992	0.000	Significant

Table 4: QSPR models are composed of statistical parameters for M₂(G)

Physical property	N	A	b	r	r2	F	P	Indicator
Boiling Point	10	236.936	1.962	0.966	0.934	113.13	0.000	Significant
Flash Point	10	102.628	1.074	0.889	0.79	30.094	0.001	Significant
Molar Volume	14	59.334	1.167	0.969	0.939	186.258	0.000	Significant
Enthalpy of Vaporization	10	49.009	0.256	0.967	0.935	115.533	0.000	Significant
Molar Refractivity	14	16.666	0.453	0.979	0.958	274.362	0.000	Significant
Polarization	14	6.586	0.18	0.979	0.958	273.318	0.000	Significant

Table 5: QSPR models are composed of statistical parameters for R(G)

Physical property	N	A	b	r	r2	F	P	Indicator
Boiling Point	10	195.489	29.927	0.957	0.915	86.31	0.000	Significant
Flash Point	10	76.88	16.593	0.891	0.794	30.81	0.001	Significant
Molar Volume	14	10.216	19.812	0.986	0.973	434.348	0.000	Significant
Enthalpy of Vaporization	10	44.195	3.858	0.948	0.898	70.31	0.000	Significant
Molar Refractivity	14	-2.236	7.678	0.995	0.99	1169.521	0.000	Significant
Polarization	14	-0.91	3.044	0.995	0.99	1158.858	0.000	Significant

Table 6: QSPR models are composed of statistical parameters for H(G)

Physical property	N	A	b	r	r2	F	P	Indicator
Boiling Point	10	199.599	31.067	0.957	0.915	86.1	0.000	Significant
Flash Point	10	80.08	17.16	0.888	0.788	29.676	0.001	Significant
Molar Volume	14	12.916	20.557	0.988	0.976	478.488	0.000	Significant
Enthalpy of Vaporization	10	44.885	3.994	0.945	0.893	66.46	0.000	Significant
Molar Refractivity	14	-1.166	7.965	0.996	0.992	1470.618	0.000	Significant
Polarization	14	-0.486	3.158	0.996	0.992	1456.932	0.000	Significant

Table 7: QSPR models are composed of statistical parameters for ABC(G)

Physical property	N	A	b	r	r2	F	P	Indicator
Boiling point	10	209.78	17.679	0.964	0.928	103.809	0.000	Significant
Flash point	10	85.29	9.782	0.896	0.802	32.418	0.000	Significant
Molar volume	14	22.046	11.594	0.982	0.964	322.916	0.000	Significant
Enthalpy of Vaporization	10	45.826	2.288	0.958	0.918	89.464	0.000	Significant
Molar Refraction	14	2.146	4.501	0.992	0.984	743.403	0.000	Significant
Polarization	14	0.828	1.785	0.992	0.984	738.398	0.000	Significant

Table 8: QSPR models are composed of statistical parameters for SO(G)

Physical property	N	A	b	r	r2	F	P	Indicator
Boiling Point	10	223.478	3.399	0.965	0.93	106.918	0.000	Significant
Flash Point	10	93.812	1.873	0.893	0.797	31.43	0.001	Significant
Molar Volume	14	38.7	2.149	0.977	0.955	254.795	0.000	Significant
Enthalpy of Vaporization	10	47.397	0.442	0.963	0.927	101.288	0.000	Significant
Molar Refractivity	14	8.632	0.834	0.987	0.974	457.203	0.000	Significant
Polarization	14	3.4	0.331	0.987	0.974	454.834	0.000	Significant

Table 9: QSPR models are composed of statistical parameters for N(G)

Physical property	N	A	b	r	r2	F	P	Indicator
Boiling Point	10	216.901	5.621	0.966	0.933	110.592	0.000	Significant
Flash Point	10	90.598	3.092	0.892	0.796	31.238	0.001	Significant
Molar Volume	14	32.14	3.596	0.98	0.961	293.345	0.000	Significant
Enthalpy of Vaporization	10	46.697	0.728	0.961	0.924	96.828	0.000	Significant
Molar Refractivity	14	6.075	1.396	0.99	0.98	600.367	0.000	Significant
Polarization	14	2.386	0.553	0.99	0.98	596.767	0.000	Significant

Table 10: QSPR models are composed of statistical parameters for N₁(G)

Physical property	N	A	b	r	r2	F	P	Indicator
Boiling Point	10	195.419	13.878	0.965	0.931	107.134	0.000	Significant
Flash Point	10	77.947	7.66	0.894	0.8	31.975	0.000	Significant
Molar Volume	14	15.415	8.988	0.983	0.967	349.829	0.000	Significant
Enthalpy of Vaporization	10	44.135	1.791	0.956	0.915	85.633	0.000	Significant
Molar Refractivity	14	-0.444	3.49	0.994	0.987	918.36	0.000	Significant
Polarization	14	-0.2	1.384	0.993	0.987	912.06	0.000	Significant

Table 11: QSPR models are composed of statistical parameters for N₂(G)

Physical property	N	A	b	r	r2	F	P	Indicator
Boiling Point	10	222.832	11.385	0.962	0.926	99.554	0.000	Significant
Flash Point	10	93.937	6.26	0.889	0.79	30.036	0.001	Significant
Molar Volume	14	32.648	7.363	0.981	0.962	301.289	0.000	Significant
Enthalpy of Vaporization	10	47.444	1.475	0.958	0.918	89.026	0.000	Significant
Molar Refractivity	14	6.25	2.858	0.991	0.982	646.976	0.000	Significant
Polarization	14	2.455	1.133	0.991	0.982	643.412	0.000	Significant

Table 12: Standard error of estimate for the physical features of drugs used in cervical cancer

Drugs	Boiling point	Flash point	Molar volume	Enthalpy of vaporization	Molar refractivity	Polarization
M1 (G)	72.36839	75.30847	40.28891	9.762642	11.57514	4.601425
M2(G)	71.94825	76.37654	46.99262	9.272824	15.02433	5.968222
R(G)	81.53923	75.66871	31.31902	11.64645	7.396604	2.946167
H(G)	81.6303	76.7991	29.87658	11.94378	6.602955	2.630321
ABC(G)	74.887	74.14803	36.15571	10.43953	9.250468	3.680135
SO(G)	73.86722	75.07196	40.50945	9.858617	11.73742	4.665821
N(G)	72.71383	75.25545	37.86601	10.06619	10.27418	4.085866
N1(G)	73.79794	74.5577	34.78509	10.65093	8.33542	3.316344
N2(G)	76.35413	76.43507	37.38287	10.46308	9.904175	3.93779

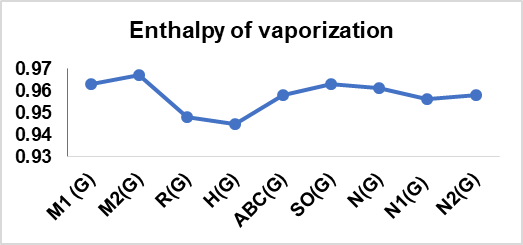
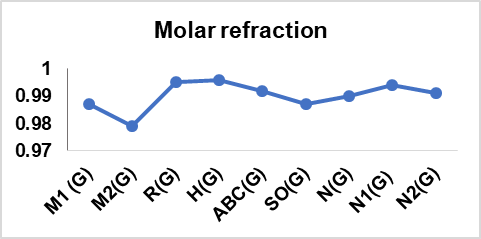
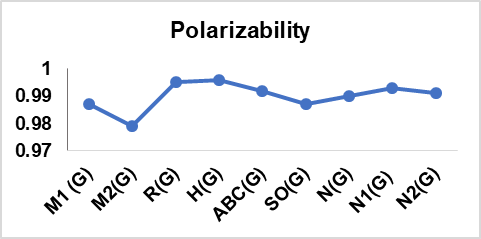
Table 13: Correlation coefficient of physical features of drugs utilized in cervical cancer

Drugs	Boiling point	Flash point	Molar volume	Enthalpy of vaporization	Molar refraction	Polarizability
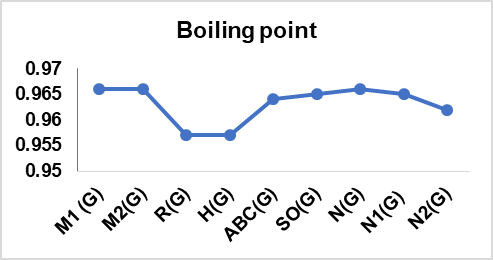
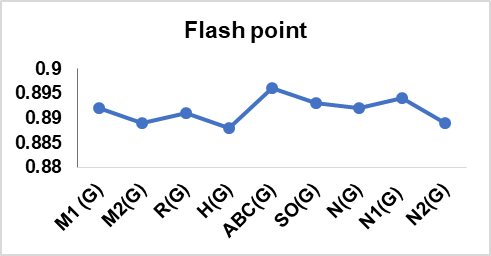
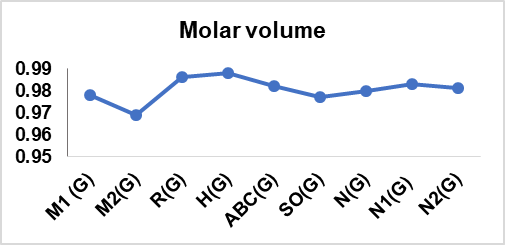
M1 (G)	0.966	0.892	0.978	0.963	0.987	0.987
M2(G)	0.966	0.889	0.969	0.967	0.979	0.979
R(G)	0.957	0.891	0.986	0.948	0.995	0.995
H(G)	0.957	0.888	0.988	0.945	0.996	0.996
ABC(G)	0.964	0.896	0.982	0.958	0.992	0.992
SO(G)	0.965	0.893	0.977	0.963	0.987	0.987
N(G)	0.966	0.892	0.98	0.961	0.99	0.99
N1(G)	0.965	0.894	0.983	0.956	0.994	0.993
N2(G)	0.962	0.889	0.981	0.958	0.991	0.991

The correlation coefficients (r>0.7) and *p values (p<0.001) observed in this study confirm strong and statistically significant relationships between computed TIs and the physical properties of the analyzed cervical cancer drugs. However, R(G), SO(G), N₁(G), and N₂(G) have slightly weaker correlations with certain properties when compared with other indices. This variation in performance can be attributed to the mathematical nature and structural information of each index that captures the chemical features that conduct the specific physical properties prediction. Conversely, the Boiling Point and enthalpy of vaporization are determined by the overall size and branching of a molecule, which helps some of the indices show superior correlations for Physical characteristics listed in the conclusion.

Table 14: Comparison of results with the survey

Indices	Boiling point	Flash point	Enthalpy of vaporization	Molar refractivity
Results of the cervical cancer drugs
M1(G)	0.966	0.892	0.963	0.987
M2(G)	0.966	0.889	0.967	0.979
H(G)	0.957	0.888	0.945	0.996
Results of schizophrenia drugs-Zhang X et al. (2023)
M1(G)	0.840	0.840	0.778	0.881
M2(G)	0.800	0.800	0.726	0.865
H(G)	0.915	0.915	0.885	0.896
Results of anti-malaria drugs-Zhang X et al.(2022)
M1(G)	0.961	0.961	0.968	0.838
M2(G)	0.962	0.963	0.978	0.76
H(G)	0.908	0.908	0.894	0.963
Results of breast cancer drugs-Shanmukha et al. (2022).
M1(G)	0.895	0.898	0.845	0.977
M2(G)	0.887	0.892	0.849	0.958
H(G)	0.873	0.874	0.793	0.993
Results of anticancer drugs-Shanmukha et al. (2022).
M1(G)	0.849	0.754	0.836	0.919
M2(G)	0.844	0.749	0.837	0.877
H(G)	0.806	0.723	0.788	0.941

There are many articles that focus on degree–based TIs and linear regression in the area of drugs. From table 14 above, we can observe the comparison of various drugs and their outcomes, and we can notice that the correlation coefficient of cervical cancer is excessive and appropriate for use as a substitute for drug experimental values.

Our analysis of cervical cancer drugs using QSPR correlates with many recent studies across various therapeutic areas that have employed degree-based topological indices. As discussed on breast cancer drugs, SO (G) and the forgotten index showed a strong correlation with the boiling point and enthalpy of vaporization, respectively. Likewise, the other study shown predictive reliability of M₁ (G) and M₂ (G) for similar properties, even for more broadly termed anticancer compounds. In this current study, these indices also provided strong predictive power, especially towards boiling point and enthalpy, during the present study, reconfirming their flexibility. The polarizability property was again well supported by our results, with correlation to H (G), which agrees with findings from the discussion on anti-malaria drugs. In addition, the correlation of ABC (G) with molar volume in our cervical cancer data parallels the results studied schizophrenia drugs that successfully employed ABC (G) and the forgotten indices.

Undoubtedly, while there are notable similarities, our study introduces novel insights by exploring the performance of N(G) and its inverse index, not received much credit in earlier QSPR investigations. These indices seem to have an extraordinarily high correlation with boiling point values, suggesting they would be good predictors for cervical cancer drug agents. The broader mapping of properties to indices implies unique structural features for cervical cancer drugs and hints at the importance of considering a more diverse range of topological descriptors for better modelling.

(i)	(ii)
(iii)	(iv)
(v)	(vi)
(vii)

Fig. 4: Graphical depiction of the correlation between Topological indices and physical properties of drugs

The standard error estimate is a measure of variance for consideration in table 12, which lies around the predicted regression line. It checks the precision of the predictions regarding the calculated regression line. Tables 15 to 20 indicate the differences between actual values and calculated values for all the physical properties of pharmaceuticals for cervical cancer.

In addition to validating the proposed models theoretically, the outcome of this study has some tangible implications for drug discovery and pharmaceutical research. The strong correlations found between topological indices and physical properties of cervical cancer treatment indicate that the established models could find application as predictive tools in the early stage of drug development.

Once molecular structure information of a new compound is obtained, it allows one to compute the topological indices of the compound. This would enable an approximate prediction of some of its important characteristics without the necessity of immediate laboratory synthesis or testing. This predictive ability greatly enhances the rapid screening of new drug candidates against the desired physical characteristics.

Moreover, these models would help in the optimization of existing compounds by facilitating the rational design of their structural modifications to improve those properties that are directly related to efficacy, safety, and stability in formulation. Therefore, these models are justified as cost-effective and efficient computational tools for lead optimization, formulation development, and screening of new drugs in pharmaceutical research.

Table 15: Contrast of actual and predicted values for Boiling point based on regression models

Drugs	BP (°C at 760 mmHg)	M1(G)	M2(G)	R(G)	H(G)	ABC(G)	SO(G)	N(G)	N1(G)	N2(G)
Ciclophosphamide	336.1±52.0	381.799	378.200	396.778	401.100	386.499	382.283	383.940	388.171	386.047
Doxorubicin	810.3±65.0	767.275	776.486	746.984	742.837	753.763	768.678	761.126	757.492	753.248
Etoposide	798.1±60.0	821.637	829.460	802.468	809.444	808.745	816.804	820.591	813.726	819.793
Fluorouracil		327.437	327.188	321.123	321.786	327.363	328.779	325.909	319.363	327.631
Gemcitabine	482.7±55.0	460.871	470.414	446.098	428.066	454.369	464.005	455.771	449.275	452.399
Hydroxyurea	222.1±23.0	263.191	264.404	263.423	263.814	263.648	264.834	261.689	257.134	268.964
Ifosfamide	336.1±52.0	381.799	378.200	396.778	401.100	386.499	382.283	383.940	388.171	386.047
Irinotecan	873.4±65.0	809.282	805.916	816.833	826.251	823.895	805.128	813.834	820.248	813.053
Methotrexate		638.783	613.640	662.859	660.416	659.923	641.096	647.014	663.954	667.371
Neratinib	757.0±60.0	722.797	694.082	775.205	783.659	751.465	719.528	739.114	767.651	738.812
Paclitaxel	957.1±65.0	1078.621	1078.634	1074.654	1062.733	1075.874	1083.595	1074.778	1065.431	1079.963
Topotecan	782.9±60.0	668.435	680.348	636.613	636.743	651.154	668.614	661.292	648.383	657.432
Vinblastine		1100.860	1139.456	1051.671	1053.196	1056.710	1100.359	1084.823	1070.774	1073.849
Vinorelbine		1058.853	1145.342	1015.040	1019.022	1017.109	1056.417	1044.846	1031.346	1036.985

Table 16: Contrast of actual and predicted values for Flash point based on regression models

Drugs name	FP (°C)	M1(G)	M2(G)	R(G)	H(G)	ABC(G)	SO(G)	N(G)	N1(G)	N2(G)
Ciclophosphamide	157.1±30.7	181.344	243.892	188.485	191.380	183.071	181.320	182.483	184.337	183.680
Doxorubicin	443.8±34.3	393.192	642.178	382.656	380.140	386.282	394.241	389.965	388.185	385.584
Etoposide	263.6±26.4	423.068	695.152	413.419	416.931	416.704	420.761	422.676	419.223	422.174
Fluorourcil		151.468	192.880	146.537	147.570	150.350	151.838	150.561	146.358	151.560
Gemcitabine	245.7±31.5	224.800	336.106	215.830	206.275	220.624	226.353	221.996	218.064	220.164
Hydroxyrea	88.1±22.6	116.160	130.096	114.546	115.550	115.096	116.601	115.235	112.011	119.303
Ifosfamide	157.1±30.7	181.344	243.892	188.485	191.380	183.071	181.320	182.483	184.337	183.680
Irinotecan	482±34.3	416.278	671.608	421.384	426.214	425.087	414.327	418.959	422.823	418.468
Methotrexate		322.576	479.332	336.013	334.614	334.359	323.938	327.195	336.556	338.365
Neratinib	411.6±32.9	368.748	559.774	398.303	402.688	385.010	367.158	377.857	393.792	377.646
Paclitaxel	532.6±34.3	564.300	944.326	564.333	556.836	564.510	567.775	562.499	558.152	565.227
Topotecan	427.3±32.9	338.872	546.040	321.461	321.538	329.507	339.102	335.048	327.962	332.900
Vinblastine		576.522	1005.148	551.589	551.568	553.906	577.012	568.024	561.102	561.866
Vinorelbine		553.436	1011.034	531.279	532.692	531.995	552.798	546.034	539.339	541.596

Table 17: Contrast of actual and predicted values for molar volume based on regression models

Drugs name	MV (cm3)	M1(G)	M2(G)	R(G)	H(G)	ABC(G)	SO(G)	N(G)	N1(G)	N2(G)
Ciclophosphamide	195.7±5.0	139.250	143.358	143.472	146.249	137.940	139.103	139.002	140.249	138.204
Doxorubicin	336.6±5.0	382.454	380.259	375.312	372.376	378.793	383.400	380.305	379.438	375.683
Etoposide	378.5±5.0	416.752	411.768	412.043	416.450	414.851	413.827	418.347	415.857	418.720
Fluorouracil	84.8±5.0	104.952	113.016	93.387	93.767	99.158	105.276	101.877	95.687	100.424
Gemcitabine	142.3±7.0	189.138	198.207	176.122	164.092	182.449	190.772	184.956	179.823	181.116
Hydroxyurea	43.9±7.0	64.418	75.672	55.189	55.407	57.373	64.847	60.793	55.385	62.483
Ifosfamide	195.7±5.0	139.250	143.358	143.472	146.249	137.940	139.103	139.002	140.249	138.204
Irinotecan	416.8±5.0	408.957	397.764	421.553	427.571	424.787	406.445	414.024	420.082	414.361
Methotrexate	295.7±3.0	301.386	283.398	319.620	317.838	317.252	302.737	307.302	318.859	320.144
Neratinib	416.8±5.0	354.392	331.245	393.994	399.388	377.286	352.325	366.223	386.017	366.347
Paclitaxel	610.6±5.0	578.888	559.977	592.233	584.051	590.036	582.504	580.962	578.873	586.979
Topotecan	281.3±5.0	320.094	323.076	302.245	302.174	311.502	320.135	316.436	308.774	313.716
Vinblastine	590±5.0	592.919	596.154	577.018	577.740	577.468	593.103	587.388	582.333	583.025
Vinorelbine	569.7±5.0	566.416	599.655	552.768	555.127	551.498	565.321	561.813	556.798	559.183

The results of this specific research will be highly useful to academics who are investing a lot of effort in modelling the intricacies of drug science in the pharmaceutical field. In addition, these findings provide a realistic approach that makes it possible to predict physical attributes associated with new findings in cervical cancer drugs, which can also be used to treat and cure a vast range of other specific medical diseases.

Here, fourteen compounds remain a meaningful starting point for validation, but in the future, an expanded dataset will be greatly beneficial to increase the robustness and generalizability of the models. In addition, applying cross-validation techniques on larger studies will help to further strengthen the predictive reliability of these models across structurally diverse drug candidates.

Over and above the shortcomings, the current results demonstrate the stated potential of the proposed approach to assist in early drug screening and structural optimization in drug research.

Table 18: Contrast of actual and predicted values for the enthalpy of vaporization based on regression models

Drugs name	EV (kj/mol)	M1(G)	M2(G)	R(G)	H(G)	ABC(G)	SO(G)	N(G)	N1(G)	N2(G)
Ciclophosphamide	57.9±3.0	68.003	67.441	70.144	70.790	68.697	68.048	68.331	69.010	68.590
Doxorubicin	123.5±3.0	118.079	119.409	115.290	114.724	116.228	118.294	117.182	116.672	116.163
Etoposide	121.7±3.0	125.141	126.321	122.443	123.287	123.343	124.552	124.883	123.929	124.784
Fluorouracil		60.941	60.785	60.391	60.593	61.043	61.090	60.815	60.130	61.021
Gemcitabine	86.2±6.0	78.275	79.473	76.502	74.257	77.480	78.675	77.634	76.896	77.186
Hydroxyurea	53.3±6.0	52.595	52.593	52.953	53.141	52.798	52.775	52.498	52.100	53.421
Ifosfamide	57.9±3.0	68.003	67.441	70.144	70.790	68.697	68.048	68.331	69.010	68.590
Irinotecan	133±3.0	123.536	123.249	124.295	125.448	125.304	123.034	124.008	124.771	123.911
Methotrexate		101.387	98.161	104.445	104.128	104.083	101.703	102.403	104.601	105.037
Neratinib	110.3±3.0	112.301	108.657	118.928	119.972	115.930	111.902	114.331	117.983	114.292
Paclitaxel	146±3.0	158.525	158.833	157.531	155.850	157.915	159.245	157.804	156.413	158.491
Topotecan	119.5±3.0	105.239	106.865	101.062	101.085	102.948	105.282	104.252	102.591	103.749
Vinblastine		161.414	166.769	154.569	154.624	155.435	161.425	159.105	157.102	157.699
Vinorelbine		155.957	167.537	149.846	150.231	150.310	155.711	153.928	152.014	152.923

Table 19: Contrast of actual and predicted values for molar refraction based on regression models

Drugs name	MR (cm3)	M1(G)	M2(G)	R(G)	H(G)	ABC(G)	SO(G)	N(G)	N1(G)	N2(G)
Ciclophosphamide	58.1±0.4	47.641	49.282	49.406	50.495	47.138	47.597	47.560	48.029	47.222
Doxorubicin	131.5±0.4	142.021	141.241	139.254	138.110	140.642	142.406	141.236	140.904	139.401
Etoposide	140.1±0.4	155.331	153.472	153.489	155.187	154.640	154.214	156.004	155.046	156.106
Fluorouracil	25.9±0.4	34.331	37.504	29.996	30.160	32.082	34.469	33.148	30.725	32.558
Gemcitabine	52.1±0.5	67.001	70.573	62.060	57.409	64.417	67.649	65.399	63.395	63.879
Hydroxyurea	13.8±0.5	18.601	23.008	15.193	15.298	15.861	18.779	17.198	15.076	17.831
Ifosfamide	58.1±0.4	47.641	49.282	49.406	50.495	47.138	47.597	47.560	48.029	47.222
Irinotecan	159.2±0.4	152.306	148.036	157.175	159.496	158.497	151.349	154.326	156.686	154.414
Methotrexate	119±0.3	110.561	103.642	117.671	116.979	116.750	111.101	112.896	117.382	117.843
Neratinib	155.1±0.4	131.131	122.215	146.495	148.576	140.057	130.346	135.769	143.459	135.777
Paclitaxel	219.3±0.4	218.251	211.003	223.321	220.126	222.650	219.676	219.133	218.344	221.417
Topotecan	112.7±0.4	117.821	119.044	110.938	110.910	114.518	117.853	116.441	113.466	115.348
Vinblastine	220.7±0.4	223.696	225.046	217.424	217.680	217.771	223.789	221.627	219.688	219.883
Vinorelbine	214.2±0.4	213.411	226.405	208.026	208.919	207.689	213.007	211.699	209.773	210.628

Table 20: Contrast of actual and predicted values for polarization based on regression models

Drugs name	POL(10-[24]cm3)	M1(G)	M2(G)	R(G)	H(G)	ABC(G)	SO(G)	N(G)	N1(G)	N2(G)
Ciclophosphamide	23±0.5	18.874	19.546	19.564	19.997	18.671	18.865	18.820	19.022	18.698
Doxorubicin	52.1±0.5	56.314	56.086	55.185	54.735	55.752	56.492	55.927	55.853	55.240
Etoposide	55.5±0.5	61.594	60.946	60.828	61.506	61.304	61.179	61.778	61.461	61.863
Fluorouracil	10.2±0.5	13.594	14.866	11.869	11.934	12.700	13.654	13.110	12.161	12.884
Gemcitabine	20.6±0.5	26.554	28.006	24.580	22.738	25.523	26.823	25.886	25.116	25.301
Hydroxyurea	5.5±0.5	7.354	9.106	6.000	6.042	6.267	7.427	6.792	5.955	7.046
Ifosfamide	23±0.5	18.874	19.546	19.564	19.997	18.671	18.865	18.820	19.022	18.698
Irinotecan	63.1±0.5	60.394	58.786	62.290	63.214	62.834	60.042	61.113	62.112	61.192
Methotrexate	47.2±0.5	43.834	41.146	46.628	46.357	46.278	44.068	44.701	46.525	46.694
Neratinib	61.5±0.5	51.994	48.526	58.055	58.884	55.520	51.706	53.762	56.866	53.804
Paclitaxel	86.9±0.5	86.554	83.806	88.514	87.253	88.275	87.160	86.785	86.563	87.754
Topotecan	44.7±0.5	46.714	47.266	43.959	43.950	45.392	46.748	46.106	44.972	45.705
Vinblastine	87.5±0.5	88.714	89.386	86.176	86.283	86.340	88.792	87.773	87.096	87.146
Vinorelbine	84.9±0.5	84.634	89.926	82.450	82.809	82.342	84.513	83.840	83.164	83.477

CONCLUSION

In this article, nine topological indices were used to develop a QSPR model for fourteen cervical cancer drugs. The model quantifies the correlation between six physical characteristics of the drugs and the TIs having been selected, as depicted in table 13. The linear regression model is validated, confirming the reliability and the extent of prediction attained. The result revealed that the boiling point has the highest correlation with M₁ (G), M₂ (G), and N (G), with r = 0.966. Flashpoint shows a good correlation with ABC (G) with r = 0.896, also molar volume has a high correlation with H (G) with r = 0.988. Also, the enthalpy of vaporization good correlation with M₂ (G) = 0.967. Both molar refraction and polarizability have a high correlation with H (G), with r = 0.996. The correlation coefficients above 0.7 and the *p-value ≤ 0.001 (**p ≤ 0.005) in all instances confirmed the statistical significance of the models, control, and indicated the robustness and reliability of the developed QSPR models.

The drugs used in cervical cancer treatment are examined in this research. Finding information about the topology of a structure using topological indices (TIs) in a shorter amount of time and at a lower cost is the goal of this effort. Using different excipients based on topological indices aids researchers and chemists in creating new drugs. By creating new medications with high correlation values, chemists can select the ideal composition for new diseases.

ACKNOWLEDGEMENT

We acknowledge the Department of Mathematics, Dr. M. G. R. Educational and Research Institute, for providing research support, and we also thank ChemSpider, https://www.chemspider.com/, for data availability for my research work.

FUNDING

Nil

AUTHORS CONTRIBUTIONS

Methodology and original draft preparation were handled by Priyadarshini S, while conceptualization and supervision were conducted by Dr. S. Kopperundevi. Both authors have reviewed and approved the final manuscript.

CONFLICT OF INTERESTS

The authors assert that they have no conflicts of interest.

REFERENCES

1. World Health Organization. Cervical cancer. In: Geneva: World Health Organization; 2024 Mar 5. Available from: https://www.who.int/news-room/fact-sheets/detail/cervical-cancer. [Last accessed on 12 Apr 2025].

2. Gadekar S, Bhadake T, Sanap G. Review on cervical cancer associated risk staging screening tests therapies and vaccination. Int J Pharm Sci. 2024;2(12):3348-65. doi: 10.5281/zenodo.14575154.

3. Jyothi BD, Sai SB, Lakshmi BC, Begum SS, Kumar DA. Awareness of cervical cancer risk assessment. Int J Pharm Pharm Sci. 2018 Feb 1;10(2):15-23. doi: 10.22159/ijpps.2018v10i2.18882.

4. Joseph AN, Dhanraj KI, Ramalingam SI, Saravanan RE. Treating cervical cancer with herbs: a review. Asian J Pharm Clin Res. 2018;11(7):4-10. doi: 10.22159/ajpcr.2018.v11i7.25580.

5. Rasheed MW, Mahboob A, Hanif I. On QSAR modeling with novel degree-based indices and thermodynamics properties of eye infection therapeutics. Front Chem. 2024 May 27;12:1383206. doi: 10.3389/fchem.2024.1383206, PMID 38860235.

6. Shanmukha MC, Usha A, Praveen BM, Douhadji A. Degree based molecular descriptors and QSPR analysis of breast cancer drugs. J Math. 2022;2022(1):5880011. doi: 10.1155/2022/5880011.

7. Shanmukha MC, Basavarajappa NS, Shilpa KC, Usha A. Degree based topological indices on anticancer drugs with QSPR analysis. Heliyon. 2020 Jun 23;6(6):e04235. doi: 10.1016/j.heliyon.2020.e04235, PMID 32613116.

8. Zhang X, Reddy HG, Usha A, Shanmukha MC, Farahani MR, Alaeiyan M. A study on anti-malaria drugs using degree-based topological indices through QSPR analysis. Math Biosci Eng. 2023 Jan;20(2):3594-609. doi: 10.3934/mbe.2023167, PMID 36899594.

9. Parveen S, Farooq FB, Awan NU, Fanja R, Choudhary MF. Topological indices of drugs used in rheumatoid arthritis treatment and its QSPR modeling. J Math. 2022 Aug;2022(1):1-11. doi: 10.1155/2022/1562125.

10. Parveen S, Awan NU, Farooq FB, Fanja R, Anjum QU. Topological indices of novel drugs used in autoimmune disease vitiligo treatment and its QSPR modeling. BioMed Res Int. 2022 Nov 15;2022:6045066. doi: 10.1155/2022/6045066, PMID 36425334.

11. Farooq FB, Parveen S, Hassan Awan NU, Fanja R. Topological descriptors and QSPR modelling of HIV/AIDS disease treatment drugs. Discrete Dynamics in Nature and Society. 2023;2023:1-13. doi: 10.1155/2023/9963241.

12. Mahboob A, Rasheed MW, Dhiaa AM, Hanif I, Amin L. Quantitative structure property relationship (QSPR) analysis of physicochemical properties and anti-hepatitis prescription drugs using a linear regression model. Heliyon. 2024 Feb 12;10(4):e25908. doi: 10.1016/j.heliyon.2024.e25908.

13. Trinajstic N. Chemical graph theory. 2^nd ed. Boca Raton (FL): CRC Press; 1992.

14. Harary F. Graph theory. 1^st ed. Reading: Addison Wesley; 1969.

15. Gutman I, Trinajstic N, Trinajstic N, Wilcox CF. Graph theory and molecular orbitals. XII. Acyclic polyenes. J Chem Phys. 1975 May;62(9):3399-405. doi: 10.1063/1.430994.

16. Randic M. Characterization of molecular branching. J Am Chem Soc. 1975 Nov;97(23):6609-15. doi: 10.1021/ja00856a001.

17. Fajtlowicz S. On conjectures of graffiti. Discrete Math. 1988;72(1-3):113-8. doi: 10.1016/0012-365X(88)90199-9.

18. Estrada E, Torres L, Rodriguez L, Gutman I. An atom-bond connectivity index: modelling the enthalpy of formation of alkanes. Indian J Chem Sec A. 1998 Oct;37A:849-55.

19. Gutman I. Geometric approach to degree-based topological indices: Sombor Indices. MATCH Commun Math Comput Chem. 2021;86(1):11-6.

20. VR K. Nirmala index. Int J Math Trends Technol. 2021 Mar;67(3):8-12. doi: 10.14445/22315373/IJMTT-V67I3P502.

21. Kulli VR, Lokesha V, Nirupadi K. Computation of inverse Nirmala indices of certain nanostructures. International Journal of Mathematics and Combinatorics. 2021 Jun 1;2:33-40.

22. S R, Kulli VR, Niranjan KM, Goudar VM. Nirmala indices of certain antiviral drugs. Int J Math Comput Res. 2023 Nov;11(11):3862-6. doi: 10.47191/ijmcr/v11i11.05.

23. Arockiaraj M, Greeni AB, Kalaam AR. Comparative analysis of reverse degree and entropy topological indices for drug molecules in blood cancer treatment through QSPR regression models. Polycyclic Aromatic Compounds. 2023;44(9):6024-41. doi: 10.1080/10406638.2023.2271648.

24. Zhang X, Saif MJ, Idrees N, Kanwal S, Parveen S, Saeed F. QSPR analysis of drugs for treatment of schizophrenia using topological indices. ACS Omega. 2023 Oct 24;8(44):41417-26. doi: 10.1021/acsomega.3c05000, PMID 37970009.

25. Parveen S, Hassan Awan NU, Mohammed M, Farooq FB, Iqbal N. Topological indices of novel drugs used in diabetes treatment and their QSPR modeling. J Math. 2022;2022(1):5209329. doi: 10.1155/2022/5209329.